‘(‘, ‘)’ 문자로만 이루어진 문자열을 괄호 문자열이라 한다. 올바른 괄호 문자열이란 다음과 같이 정의된다. ()는 올바른 괄호 문자열이다. S가 올바른 괄호 문자열이라면, (S)도 올바른 괄호 문자열이다. S와 T가 올바른 괄호 문자열이라면, 두 문자열을 이어 붙인 ST도 올바른 괄호 문자열이다. (()())()은 올바른 괄호 문자열이지만 (()은 올바른 괄호 문자열이 아니다. 괄호 문자열이 주어졌을 때 올바른 괄호 문자열인지 확인하는 방법은 여러 가지가 있다.
하지만 우리가 궁금한 것은 길이가 L인 올바른 괄호 문자열의 개수이다. 길이 L이 주어졌을 때 길이가 L인 서로 다른 올바른 괄호 문자열의 개수를 출력하는 프로그램을 만들어 보자.
입력
첫 번째 줄에 테스트케이스의 개수를 나타내는 T (1 ≤ T ≤ 100)가 주어진다. 두 번째 줄부터 각 테스트케이스마다 괄호 문자열의 길이를 나타내는 L이 주어진다. (1 ≤ L ≤ 5000)
출력
각 테스트 케이스에 대해 길이가 L인 올바른 괄호 문자열의 개수를 1,000,000,007로 나눈 나머지를 출력하시오.
==
문제 분석
일단 n이 홀수라면 절대 올바른 괄호가 될 수 없으므로 입력을 2로 나눴을 때 나머지가 1이라면 0을 answer에 추가해준다.
괄호의 길이가 2라면 만들 수 있는 것은 () 1가지이다.
괄호의 길이가 4라면 만들 수 있는 것은 ()(), (()) 2가지이다.
이후 규칙을 찾기 위해 작성해봤을 땐
괄호의 길이가 6이라면,
1 ) 괄호의 길이가 4인 것에 () 를 추가하거나 감싸주는 것.
2 ) 괄호의 길이가 2인 것에 (()) 을 추가해주기가 있었다.
처음에는 위와 같은 규칙에 따라 현재 값 기준으로 이전 짝수들에서의 조합을 찾으면 되는 줄 알았지만 이 과정이 생각보다 어려워서 답지를 보게 되었다.
이 문제는 여러가지 조합적 문제를 해결할 때 사용되는 카탈란 수를 활용하여 푸는 것이었다.
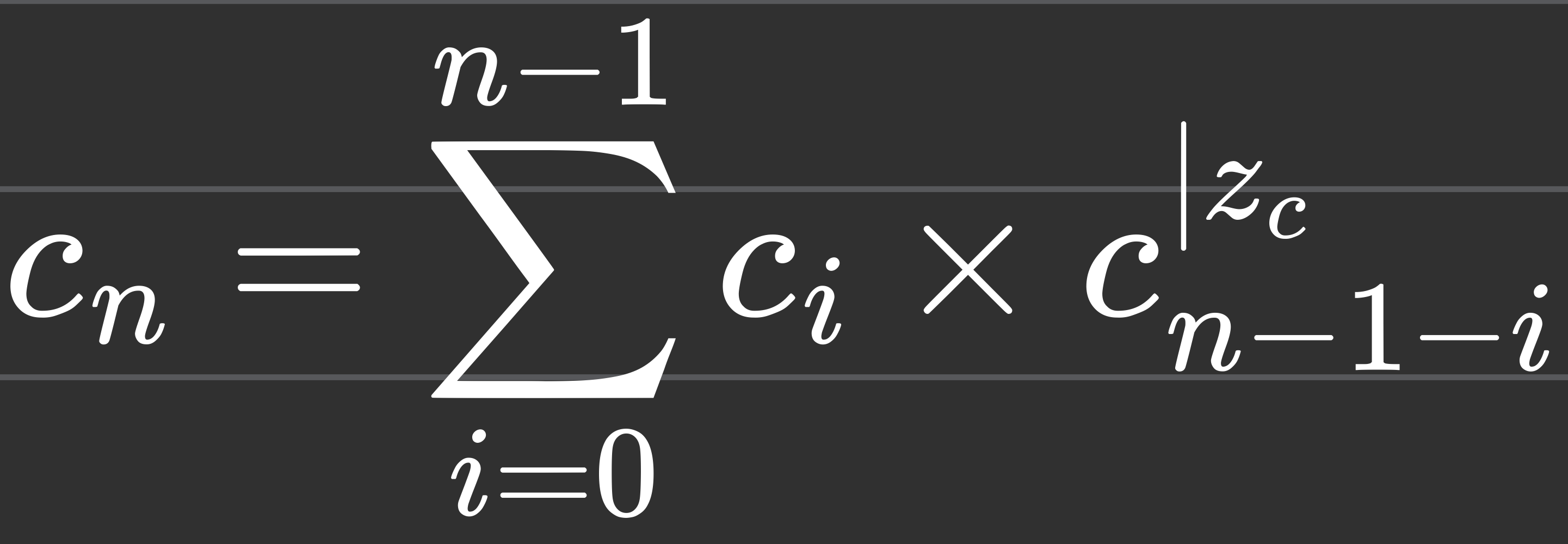
이를 코드화 하여 아래의 반복문을 만들었다.
for (let i = 2; i <= N / 2; i++) {
for (let j = 0; j < i; j++) {
dp[i] = (dp[i] + dp[j] * dp[i - 1 - j]) % INF;
}
}이 코드를 통해 n의 최댓값인 5000까지 구하여 dp에 기록했는데 정답 제출시 틀림이 나왔다.
INF가 10억인 것을 감안하여 기록되는 수를 BigInt 처리 해줬더니 정답 처리 됨.
const input = require('fs')
.readFileSync(process.platform === 'linux' ? '/dev/stdin' : './input.txt')
.toString()
.trim()
.split('\n');
const answer = [];
const T = +input.shift();
const N = 5000;
const INF = 1_000_000_007n;
const dp = Array.from({ length: N + 1 }, () => 0n);
dp[0] = 1n;
dp[1] = 1n;
for (let i = 2; i <= N / 2; i++) {
for (let j = 0; j < i; j++) {
dp[i] = (dp[i] + dp[j] * dp[i - 1 - j]) % INF;
}
}
while (input.length) {
const n = +input.shift();
if (n % 2 === 1) answer.push(0);
else {
answer.push(dp[n / 2].toString());
}
}
console.log(answer.join('\n'));'코딩 테스트 > 백준' 카테고리의 다른 글
| 1406 에디터 (자바스크립트) (0) | 2025.02.26 |
|---|---|
| 16637 괄호 추가하기 (자바스크립트) (0) | 2025.02.25 |
| 4574 스도미노쿠 ( 자바스크립트 ) (1) | 2025.02.07 |
| 20056 마법사 상어와 파이어볼 (0) | 2025.01.24 |
| 16957 체스판 위의 공 (0) | 2025.01.23 |
